什么是晶振弹性性质?石英晶振的弹性与应力有关吗?
在外力作用下,物体的大小和形状都要发生变化,通常称之为形变。如果外力撤消后,物体能恢复原状,则这种性质称为物体的弹性;如果外力撤消后,物体不能恢复原状,则这种性质就称为物体的塑性。自然界既不存在完全弹性的物体,也不存在完全塑性的物体。对于任何物体,当外力小时,形变也小,外力撤消后,物体可完全复原;当外力大时,形变也大。若外力过大,形变超过一定限度,物体就不会复原了。这就说明,物体有一定的弹性限度,超过这个限度就变成塑性。与压电有关的问题,都属于弹性限度范围内的问题。因此,这里仅讨论物体的弹性性质。
一、应力
选两根长度相等,粗细不同的橡皮绳,当这两根橡皮绳受到相同的拉力作用时,显然,细橡皮绳比粗橡皮绳拉得长一些。为什么在相同的外力作用下,它们的伸长量不一样呢?这是因为两根橡皮绳的粗细不一样,也就是横截面的大小不样。由此可见,在拉力的作用下,物体的伸长量不仅与力的大小有关,而且还与物体的横截面的大小有关。为了计入横截面大小的影响,引入单位面积的作用力(即应力)这个概念,它的数学表达式为:
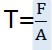
式中,T为应力,F为作用力,A为横截面(即力的作用面积)。通常规定作用力为拉力时,T>0,作用力为压力时,T<0。
二、应变
选择两根长度不等,但粗细相同的橡皮绳,当这两根橡皮绳受到相同的拉力作用时,它们的应力相同,而伸长量不同,即长橡皮绳比短橡皮绳拉得长一些。由此可见,物体的伸长量不仅与应力有关,而且还与原来的长度有关。为了计入长度的影响,引入单位长度的伸长量(即应变)这个概念。它的数学表达式为
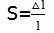 (2.2.2)
(2.2.2)
式中,S为应变,l为原长,△l为伸长量,△l为单位长度的伸长量(或相对伸长量)。
三、正应力与正应变
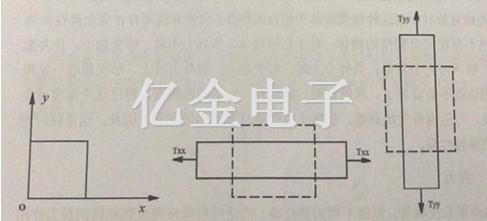
如图2.2.1(a)所示的小方片,当它受到x方向的应力作用时,除在x方向产生伸长外,同时在y方向也产生收缩,如图2.2.1(b)所示。同样,当小方片受到y方向的应力作用时,除了在y方向产生伸长外,同时在x方向也产生收缩
如图2.2.1(c)所示。上述
(a)未受力情况(b)沿x方向受力时的形变情况(c)沿y方向受力时的形变情况
图2.2.1小方片应力、应变示意图
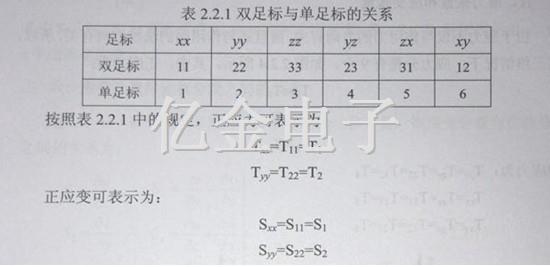
沿x方向应力和y方向应力的特点是,力的方向与作用面垂直(或力的方向与作用面的法线方向平行)。为了反应这两个方向在应力符号上要附加两个足标,例如Tx和Ty。应力的第一个足标表示力的方向,第二个足标表示作用面的法线方向。同理,应变也有两个足标,例如Sx和Sy应变的第一个足标表示原长度的方向,第二个足标表示伸长量的方向,Tx、Ty又称正应力(或伸缩应力),Sx、Sy又称为正应变(或伸缩应变)为了简便,通常将足标中的(x,y,z)用(1,2,3)表示,而且将双足标简化为单足标,双足标与单足标的关系如表2.2.1所示。
四、切应力与切应变
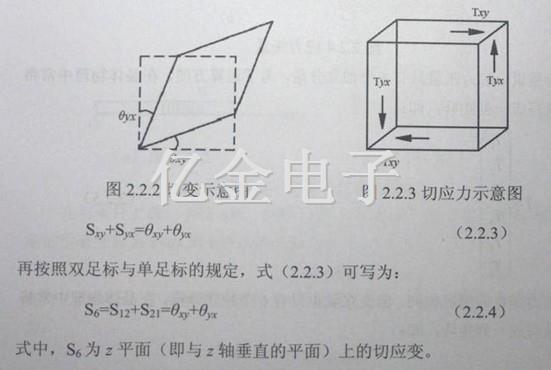
形变前为一正方形的薄片,在形变后变为菱形,这样的形变称为石英晶振晶体的切变,如图22.2所示。从图中看出,切变的特点是形变前、后四个边之间的夹角发生了变化,一个对角线被拉长,另一个对角线被压缩。而且角度6xy和eyx的变化越大,切变越大。因此切应变与这两个角度之间的关系为:
显然,S6这种切应变,在如图2.2.3所示的两对应力(Tyx,Tyx和Txy,Tyx)的作用下产生的,而这两对应力称为切应力。石英晶振,有源晶振,石英晶体谐振器等压电水晶元件切应力的特点是:力的方向与作用面平行,它可以使物体产生切变,而不能使物体产生转动,故有:
Tyx= Txy = T21 = T12 =T6
五、应力张量和应变张量
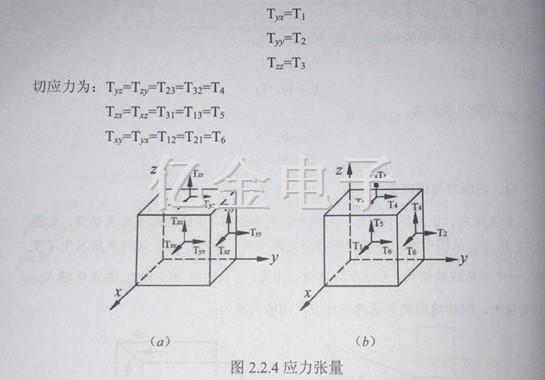
由于应力不仅与作用力的方向有关,而且还与作用面的法线方向有关,所以,在三维情况下,应力分量有9个,如图224所示。其中,正应力为:
这就是说,应力张量只有6个独立分量,为了运算方便,在晶体物理中常将应力张量写成一列矩阵,即:

与应力张量的情况相同,应变张量也只有6个独立分量。在晶体物理中常将应变张量写成一列矩阵,即:

式中S1、S2、S3分别表示沿x、y、z方向的正应变;S4、S5、S6分别表示沿x、y、z平面的切应变。
六、应变分量与位移分量之间的关系
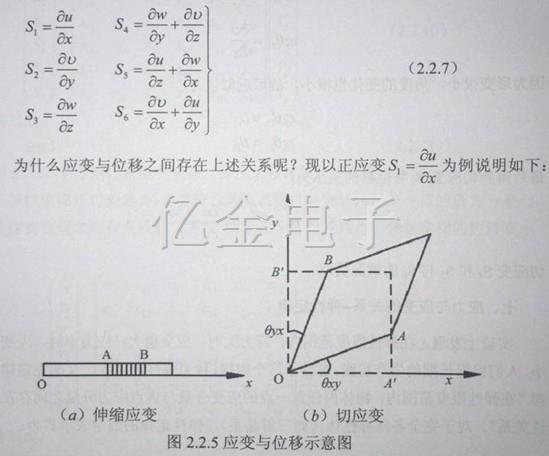
设u、v、w分别表示沿x、y、z方向的位移分量,则应变分量与位移分量之间的关系为:
在石英晶振杆上选一小段AB,如图22.5(a)所示,若A端的位置坐标为x,B端的位置坐标为x+dx,则AB小段的原长为:
x+dx-r=dx
在外力作用下,若A端的位移为u,B端的位移为u+dh,则AB两端的相对位移为:
u+du-u=du
当da=0时,它表示AB两端的位移相等,即原长不变。当dh≠0时,它表示AB两端的位移不等.即AB段的长度发生了变化,而dh就是等于它沿x方向的伸长量。根据正应变的定义:沿x方向的正应变S1等于x方向的伸长量与x方向上的原长之比,即得到S1=![]() 正应变S2和S3与S1的情况类似。再以切应变S6为例。根据切应变的定义:
正应变S2和S3与S1的情况类似。再以切应变S6为例。根据切应变的定义:
切应变S4和S5与S6的情况类似。
七、应力与应变的关系一弹性定律
实验上发现,在弹性限度范围内,有源晶振,石英晶体振荡器应力大时,应变也大;应力小时,应变也小。人们根据长期的生产实践,总结了这个规律,称为弹性定律或广义胡克定律,即“在弹性限度范围内,物体内任意一点的应变分量与该点应力分量之间存在线性关系”。对于完全各向异性体(如三斜晶系),弹性定律的数学表示式为:
式中系数S称为弹性柔顺常数,并有Sij=Sji(i≠j),由式(2.2.8)可以看出不仅正应力能产生正应变,而且切应力也能产生正应变;同样,不仅切应力能产生切应变,而且正应力也能产生切应变。这就是说,在一般情况下,应变与应力之间的关系是比较复杂的。
相关资讯
- [2024-11-09]温度补偿晶体振荡器 JT21LE,功耗极低...
- [2023-06-26]Rakon推出RakonXpress品牌的现成频率...
- [2023-06-20]Cardinal晶振公司环境政策,CSM1Z-A0B...
- [2023-06-20]Cardinal晶振ROSH证明,CX532Z-A2B3C5...
- [2023-06-17]为什么选择ClearClock有源晶振,AK2AD...
- [2021-01-21]低功耗性能且含数字温度补偿的时钟IC...
- [2020-12-04]TXC晶振车规级频率组件最新产品应用方...
- [2020-10-19]石英振荡器系列六——产品未来应用市...






 销售代表
销售代表
